I started my research with 10 individuals(NT) with a Carrying Capacity (K) of 10000 and the rate of increase(r) at .11 for 100 years. Midway I changed the Carrying Capacity (K) to 20000 and the rate of increase (r) at .1 for another 100 years. I noticed in the graph a dent was shown and the number of individuals continued to increase. This is important because the graph shows by increasing the rate and carrying capacity the number of individuals still continue to grow. Complexity models allow for you to thoroughly map trends like populations growth etc. These models are also quicker, easier and more efficient.
April 4, 2012
Population Growth
In this Logistic model I used the same formula which was
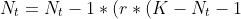/K))+N_{t}-1)
I started my research with 10 individuals(NT) with a Carrying Capacity (K) of 10000 and the rate of increase(r) at .11 for 100 years. Midway I changed the Carrying Capacity (K) to 20000 and the rate of increase (r) at .1 for another 100 years. I noticed in the graph a dent was shown and the number of individuals continued to increase. This is important because the graph shows by increasing the rate and carrying capacity the number of individuals still continue to grow. Complexity models allow for you to thoroughly map trends like populations growth etc. These models are also quicker, easier and more efficient.
I started my research with 10 individuals(NT) with a Carrying Capacity (K) of 10000 and the rate of increase(r) at .11 for 100 years. Midway I changed the Carrying Capacity (K) to 20000 and the rate of increase (r) at .1 for another 100 years. I noticed in the graph a dent was shown and the number of individuals continued to increase. This is important because the graph shows by increasing the rate and carrying capacity the number of individuals still continue to grow. Complexity models allow for you to thoroughly map trends like populations growth etc. These models are also quicker, easier and more efficient.
Labels:
population growth,
student
Subscribe to:
Post Comments (Atom)

No comments:
Post a Comment