Population Growth Model

Equations:

Population

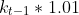Increasing k

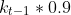Decreasing k

This graph shows varying carrying capacities of sparrows in a particular area.  The carrying capacity increases at a constant rate for ten years and then decreases the next ten years.  The varying carrying capacity can be caused by the areas inhabitants wanting to construct new housing developments.  In their minds they think cutting trees in ten year intervals is sufficient enough to not cause any harm to the sparrows.  In actuality we can see by the graph that the sparrow population will be extinct if an event like this were to be continued.  On the graph we can see the fluctuating k-value and we see that the number of individuals fluctuates accordingly, but it is delayed at first.  The number of individuals does catch up to the lowered k-value as the years progress.  The reason behind this is that, although the carrying capacity has been lowered, the number of individuals won't tie off instantly, therefore after many years the graphs do almost become identical.  We should care because even though it may seem that the resources are being replenished, there may be some underlying problems.  We started off simple by having each pair of birds have 10 offspring and observing the results.  Next, we had a rate of increase of .1 as well as .11 on the population of the sparrows. We graphed the data and saw the difference in the two.  Next we incorporated a carrying capacity and we saw the number of individuals reach the capacity and level off.  Then I put all these things together and modeled a population in an environment with a varying carrying capacity.  Once again just like everything in biology simple things join together to become very complex.  Going from simplicity to complexity is ideal in science because it is much easier to control a smaller sample than a larger one.  Once the the sample has been perfected we can scale up.  The equations used were the population equation that takes carrying capacity into account and the two others were used to maintain a constant increase or decrease of the k-value over the respective 10 year interval.